Introduction

Like a lot of folks stuck at home during lockdown, I’m currently spending my newfound free time on a personal project. I’m developing it in Rust because I need fast execution speed and memory efficiency, although guaranteed memory safety is certainly a great perk.

The program I’m building is a phylogenetic inference tool (used to estimate evolutionary trees), so there’s a lot of constructing and modifying tree data structures. Naturally, tree traversals are fundamental to many of the algorithms I’ll use, but implementing one in Rust was not as easy as I expected.

In this article I’ll walk through how a traditional pre-order traversal is implemented in Python, to set a reasonable baseline for comparison. Then we’ll port the same code over to Rust.

We’ll first implement an immutable traversal, and follow with an attempt to develop a mutable traversal. The issues we’ll encounter with these two Rust programs will lead us to our final solution using arena allocators and the visitor pattern. Eventually, we’ll develop an implementation that will be more memory-safe and flexible than the original Python code.

The lessons learned from this exercise will obviously be useful when writing other tree traversals, but they can also be generalized to graph traversal algorithms as well.

Don’t Shoot the Messenger

I really enjoy what Rust brings to the table, and I think the memory ownership model is a great abstraction once you get used to it. But when starting out, it’s difficult to wrap your head around why code that just works in one language won’t just work when ported to Rust. I think everyone goes through this “fighting the borrow-checker” stage before they start to enjoy the language, but there are some particularly difficult habits to break before you get there.

There was definitely a point at which I became extremely frustrated with the language. After all, what good is Rust if I can’t even implement a simple tree traversal? It begged the question: what else would the language restrict me from in the future?

It’s at these moments that it’s important to realize that the borrow-checker isn’t stupid. It’s complaining for a reason, and probably a very good one. It isn’t the language that’s denying you because of its limitations; it’s just recognizing that there’s a memory-safety issue in your code. It’s forcing you to think differently about your problem, and to be more conscious about memory-safety.

Hopefully this article will show just how useful the borrow-checker is in helping us write safe, fast programs. Yes, it will be incredibly frustrating at times, but I think the end result is well worth the trouble.

Before we continue it will be relevant and useful to learn the memory ownership rules I mentioned before. If you’re already familiar with these, feel free to skip ahead to the next section, in which we’ll write a pre-order traversal in Python.

Reviewing Rust Memory Ownership Rules

This will be an informal review for those who don’t already know the ownership rules, and a more thorough reference can be found in the Rust Book 2nd Ed.

Type-safety and memory-safety are laudable goals, and preventing user error is one of the prime benefits of choosing Rust. But as always, rules are restricting. You’ll definitely feel limited at first because you won’t have access to all the tools and methods you’ve used before. We’ll see that this is a good thing, eventually, as we’ll learn how to write memory-safe code.

1. All data, such as values and references, will have one owner.

   let x = 5;  // here `x` is the owner of the data
   

   Typically when the scope of the owner ends, the owned memory is de-allocated.

2. Ownership of data can be transferred by a move operation.

   fn add(x: usize, y: usize) -> usize {
       let sum = x + y;  // `sum` owns the value of `x + y`
       return sum;       // the value is moved out from `sum` as returned data
   }
   

   The original owner also does not have access to moved data if it was moved to a new owner.

   let x = Box::new(5);
   let y = x;          // move occurs here
                       // `y` is now the owner of the data
   
   println!("{}", x);  // ILLEGAL: will not compile because data was moved out of `x`
   

3. An owner can lend the owned data out as borrowed references. A borrow is an immutable (read-only) reference to data.

   You can have as many immutable borrows as you want. As long as the data is being borrowed, it won’t be de-allocated.

   let x = 5;
   
   let y = &x;  // `&` signifies an immutable borrow
   let z = &x;  // borrow again
   

4. A mutable borrow is a read-write reference to data. You can only have one mutable borrow to owned data at a time.

   let mut x = 5;  // `mut` specifies that owned data can be mutated
   let y = &x;
   
   let z = &mut x;  // `&mut` signifies a mutable borrow
                    // `y` cannot be used anymore because `x` was mutably borrowed
   z += 1;
   
   println!("{}", y);  // ILLEGAL: will not compile due to the mutable borrow
   

   As I noted in the comment above, this code will not compile because mutable borrows can’t be used simultaneously with immutable borrows. When a mutable borrow occurs, all immutable borrows up to that point should be considered stale.

   One could change the data using a mutable borrow, so in order to avoid a data race the previous immutable borrows should be discarded.

   To preserve program soundness, we must re-borrow to get a new read-only reference, as shown below.

   let mut x = 5;
   let y = &x;
   
   let z = &mut x;     // `&mut` signifies a mutable borrow
                       // `y` cannot be used anymore because `x` was mutably borrowed
   z += 1;
   
   let y = &x;         // borrow again from `x`
   println!("{}", y);  // works because `x` is borrowed again after the modification
   

These rules are great in theory. But when we start building complicated programs with the same mindset as before, we’ll quickly run into issues. We have to be mindful of ownership and borrowing every step of the way.

A Motivating Example in Python

As an example, let’s examine how a simple pre-order traversal of the depicted tree can be implemented in Python 3. This will give us a baseline to compare to when we implement the same thing in Rust.

As part of the traversal, I want to visit every node, so that I can mutate each node’s internal data.

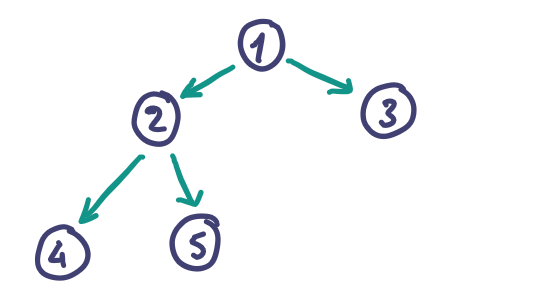
Tree Node

This class represents a node in the tree. An instance holds an arbitrary value and the child node references for the left and right subtrees.

1class TreeNode:
2    value = None
3    left  = None
4    right = None
5
6    def __init__(self, value, left, right):
7        self.value = value
8        self.left  = left
9        self.right = right

Tree

This class represents the tree structure itself. In our example it only tracks the root node. We also implement the __iter__ function to return the pre-order iterator instance that we’ll define next.

1class Tree:
2    root = None
3
4    def __init__(self, root):
5        self.root = root
6
7    def __iter__(self):
8        return TreePreorderIter(self.root)

Pre-order Traversal

This class holds the logic for performing a pre-order traversal over the tree nodes. It implements the __next__ handler so that we can use the iterator in loops.

 1class TreePreorderIter:
 2    stack = []
 3
 4    def __init__(self, root):
 5        if root is not None:
 6            self.stack = [root]
 7
 8    def __next__(self):
 9        if len(self.stack) > 0:
10            n = self.stack.pop()
11
12            if n.right is not None:
13                self.stack.append(n.right)
14
15            if n.left is not None:
16                self.stack.append(n.left)
17
18            return n
19        else:
20            raise StopIteration

Running a Simple Test

In our test, we’ll build the example tree depicted above and then confirm two things: that we can iterate through every node, and that we can modify the tree during iteration. First, we’ll update the contents of the tree during the first iteration, as seen at line 10, by multiplying the node values by 10. Then in our second pass we’ll print the updated value of each node.

It’s certainly a contrived example, but it fits my use case regarding the implementation of branch-swapping algorithms.

 1a = TreeNode(4, None, None)
 2b = TreeNode(5, None, None)
 3c = TreeNode(2, a, b)
 4d = TreeNode(3, None, None)
 5e = TreeNode(1, c, d)
 6
 7tree = Tree(e)
 8
 9for node in tree:
10    node.value *= 10
11
12for node in tree:
13    print(node.value)

You can see the output for yourself by running the script below. The printed values should be 10, 20, 40, 50, and 30 in that order.

Can we take a moment to appreciate how easy Python makes it for us? Simple, succint, and tidy. Nothing really special to see here, and that’s the point! Unfortunately, it won’t be so simple in Rust.

An Immutable Traversal in Rust

Recall that in Rust, we have two different kinds of references: immutable and mutable borrows. Like in Python, we preserve the Tree’s ownership of all the TreeNodes. In other words, the tree struct holds all the references to its nodes. But unlike in Python, we have to decide whether the reference we return during iteration will be immutable or mutable.

To get an accurate rewrite of our Python code, we eventually need to use mutable references so that we can modify the node values as we traverse. For now, however, let’s start with the simpler case of a read-only traversal. If we can get that working, then the mutable implementation should require just a few changes.

Tree Node

 1pub struct TreeNode {
 2    pub value: usize,
 3    pub left:  Option<Box<TreeNode>>,
 4    pub right: Option<Box<TreeNode>>
 5}
 6
 7impl TreeNode {
 8    pub fn new(
 9                value: usize,
10                left: Option<Box<TreeNode>>,
11                right: Option<Box<TreeNode>>
12              ) -> Self {
13        TreeNode {
14            value,
15            left,
16            right
17        }
18    }
19}

The above code is an example of how we explicitly reason about null-able types through the use of Option. An Option can either be None (null) or Some, where Some is a container for a non-null value.

The Box signifies that the data being wrapped/boxed is going to be stored on the heap, and the box acts as a pointer that we can de-reference later. As our node structure is recursive through its left and right fields (a TreeNode has references to other TreeNodes), we use the Box to inform the compiler of the TreeNode’s byte-size at compile-time. Otherwise we’d get a compiler error, as it won’t be able to infer the size by itself.

Tree

The following code is very similar to the Tree class definition we observed in Python.

 1pub struct Tree {
 2    root: Option<TreeNode>
 3}
 4
 5impl Tree {
 6    pub fn new(root: Option<TreeNode>) -> Self {
 7        Tree {
 8            root
 9        }
10    }
11
12    pub fn iter(&self) -> PreorderIter {
13        PreorderIter::new(self.root.as_ref())
14    }
15}

The as_ref() function on line 13 is used to borrow the contents of the Option type. In this case, self.root.as_ref() will return data of the type Option<&Box<TreeNode>>, signifying that the Box is borrowed instead of the Option itself (&Option<Box<TreeNode>>).

Immutable Pre-order Traversal

As we can see, Rust is more verbose than Python, but the similarities in the code are still visible. On line 19, we see that the Iterator trait is being implemented for the data structure, and then we implement the next function on line 21 just as we did in Python.

 1pub struct PreorderIter {
 2    stack: Vec<&TreeNode>
 3}
 4
 5impl PreorderIter {
 6    pub fn new(root: Option<&TreeNode>) -> Self {
 7        if let Some(node) = root {
 8            PreorderIter {
 9                stack: vec![node]
10            }
11        } else {
12            PreorderIter {
13                stack: vec![]
14            }
15        }
16    }
17}
18
19impl Iterator for PreorderIter {
20  type Item = &TreeNode;
21
22  fn next(&mut self) -> Option<Self::Item> {
23      if let Some(node) = self.stack.pop() {
24          if let Some(right) = &node.right {
25              self.stack.push(&right)
26          }
27
28          if let Some(left) = &node.left {
29              self.stack.push(&left)
30          }
31
32          return Some(node)
33      }
34
35      return None
36  }
37}

One thing to be aware of is that Rust forces us to be explicit about how null-able types are handled. Just as we defined data to be Optional, we have to unwrap the Option when we want to use its contents. On line 22, we can see how we unwrap the Option within the conditional statement by unpacking the Some value.

Unfortunately, the code as it is written right now will not compile. Try it for yourself below.

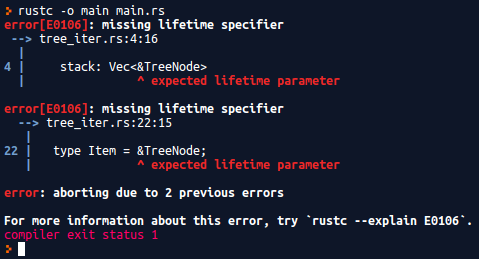
You should encounter errors for missing lifetime parameters. We haven’t done anything special yet, but we’ve already hit our first road-block! Let’s take a closer look.

Lifetimes

Typically the borrow-checker is able to automatically reason about some data’s lifetime, or how long it lives for before it can be de-allocated from memory. For example, when some owner of data goes out of scope, then the lifetime of the data could end at that point too, so the compiler might be able to free that memory.

However, the compiler will not free data that is still being borrowed. This is to avoid dangling reference issues often encountered in languages like C or C++, in which data is freed but pointers still point to the inaccessible memory. Thus borrows have lifetimes as well, so that the compiler can determine when a borrow ends and when the borrowed data can eventually be freed.

This makes sense, because we don’t want the tree nodes to be freed while they’re still being borrowed by the iterator! The question the compiler is then asking is: What is the lifetime of the borrow? In other words, when will the borrow end?

We know that when the PreorderIter struct borrows some data, that borrow should live for as long as the struct lives for. But when we use a trait like Iterator, which contains generic parameters like type Item, we introduce ambiguity that the compiler can’t resolve without help.

We can eliminate this ambiguity by explicitly annotating the lifetimes of each ambiguous reference. A lifetime is denoted by an apostrophe ' followed by the lifetime identifier (some unique name for the lifetime). For example 'a signifies a lifetime a.

We can then explicitly annotate a struct’s lifetime by attaching <'a> to the end of it, like so: PreorderIter<'a>. Then we can use the lifetime 'a anywhere within that struct’s scope to annotate borrows.

When implementing functions or traits on the struct, we have to first declare the lifetime for that implementation like this: impl<'a>. Then it can be used throughout that scope such as when annotating the struct or borrows.

 1pub struct PreorderIter<'a> {  // explicitly annotate the lifetime of the struct
 2    stack: Vec<&'a TreeNode>   // specify that the borrow lives for as long as the struct lives
 3}
 4
 5impl<'a> PreorderIter<'a> { // declare the lifetime and apply as lifetime of the struct
 6    pub fn new(root: Option<&'a TreeNode>) -> Self { // annotate lifetime of the borrow
 7        if let Some(node) = root {
 8            PreorderIter {
 9                stack: vec![node]
10            }
11        } else {
12            PreorderIter {
13                stack: vec![]
14            }
15        }
16    }
17}
18
19impl<'a> Iterator for PreorderIter<'a> {
20  type Item = &'a TreeNode;
21
22  fn next(&mut self) -> Option<Self::Item> {
23      if let Some(node) = self.stack.pop() {
24          if let Some(right) = &node.right {
25              self.stack.push(&right)
26          }
27
28          if let Some(left) = &node.left {
29              self.stack.push(&left)
30          }
31
32          return Some(node)
33      }
34
35      return None
36  }
37}

With the lifetimes explicitly annotated, we’ve removed any ambiguities the compiler may encounter with these borrowed references and made it clear that the borrows will live for as long as the PreorderIter struct lives.

For a more in-depth treatment of these concepts, please see Arthur Liao’s article "Rust Borrows and Lifetimes".

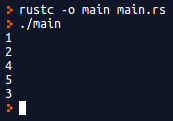
Now that we have lifetimes addressed and our code successfully compiles, let’s write the main routine to test the iterator.

Running the Test

Pay special attention to the different loop implementations. They’re equivalent, with the only difference being that the while loop on line 16 is more explicit about the iteration. We’ll use these while loops again later.

 1fn main() {
 2    let a = TreeNode::new(4, None, None);
 3    let b = TreeNode::new(5, None, None);
 4    let c = TreeNode::new(2, Some(Box::from(a)), Some(Box::from(b)));
 5
 6    let d = TreeNode::new(3, None, None);
 7    let e = TreeNode::new(1, Some(Box::from(c)), Some(Box::from(d)));
 8
 9    let tree = Tree::new(Some(e));
10
11    for _node in tree.iter() {
12        // _node.value *= 10;
13    }
14
15    let mut iterator = tree.iter();
16    while let Some(node) = iterator.next() { // equivalent to the for loop construction
17        println!("{}", node.value)
18    }
19}

Try un-commenting line 17 and re-running the test (hint: it won’t work). Recall that we can’t mutate data through immutable borrows. We need to make a mutable iterator instead that returns mutable borrows.

A Failed Attempt at Mutable Traversal

With the immutable iterator working, we now have the foundation to start implementing a mutable one. The easiest way may be to simply update our immutable iterator to use mutable borrows.

We don’t need to change our TreeNode, but we do have to update the Tree and PreorderIter structs to take mutable references instead of plain old immutable ones.

Tree

 1pub struct Tree {
 2    root: Option<TreeNode>
 3}
 4
 5impl Tree {
 6    pub fn new(root: Option<TreeNode>) -> Self {
 7        Tree {
 8            root
 9        }
10    }
11
12    pub fn iter(&mut self) -> PreorderIter {
13        PreorderIter::new(self.root.as_mut())
14    }
15}

Like as_ref(), the as_mut() function returns a borrow of the Option’s contents, only this time it’s a mutable borrow.

Mutable Pre-order Traversal

Wherever we used an immutable borrow before, we’ll change it to be a mutable borrow instead.

 1pub struct PreorderIter<'a> {
 2    stack: Vec<&'a mut TreeNode>
 3}
 4
 5impl<'a> PreorderIter<'a> {
 6    pub fn new(root: Option<&'a mut TreeNode>) -> Self {
 7        if let Some(node) = root {
 8            PreorderIter {
 9                stack: vec![node]
10            }
11        } else {
12            PreorderIter {
13                stack: vec![]
14            }
15        }
16    }
17}
18
19impl<'a> Iterator for PreorderIter<'a> {
20  type Item = &'a mut TreeNode;
21
22  fn next(&mut self) -> Option<Self::Item> {
23      if let Some(node) = self.stack.pop() {
24          if let Some(right) = &mut node.right {
25              self.stack.push(right)
26          }
27
28          if let Some(left) = &mut node.left {
29              self.stack.push(left)
30          }
31
32          return Some(node)
33      }
34
35      return None
36  }
37}

Running the Test Again

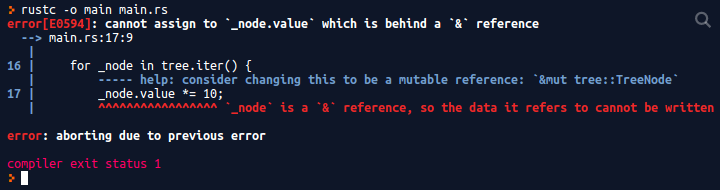
Heads up! It’s not going to work. Run it for yourself below and let’s see what our mistake is.

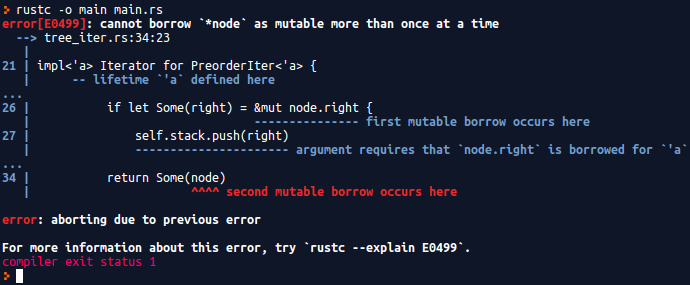
Uh oh. Apparently we’re mutably borrowing the node in the next routine twice. How is this happening? 😫

Why It Doesn’t Work

At first glance, the error output seems pretty self-explanatory. We’re mutably borrowing the same data twice, and according to the rules we discussed, we should be only mutably borrowing once!

Well, let’s take a look at what’s being borrowed.

1. We first borrowed a node (like the root node) when we put in on the stack.
2. At line 26, we take it off the stack and get the borrow back.
3. We then borrow its child and put that on the stack at line 27.
4. Finally, at line 34, we return the borrow reference of node.

It may help to think about this in a physical sense. Let’s imagine you’re holding onto a leaf (step 3), while you also need to give the stick it’s attached to, to someone else (step 4). That can’t happen without either you giving up the leaf, or the other person not getting the stick!

So in order to return the data, the compiler assumes a second borrow occurs. The only way to return the parent node is to borrow it again, which we aren’t allowed to do.

So why is this not allowed? If we were able to return the second mutable reference, that would allow some other process to mutably borrow the same child node that our iterator already has on the stack! The other process could mutate it at the same time we do, which would lead to a data race.

If Python were not garbage-collected, this memory unsafety would be apparent there too. Rust not only forces us to be conscious of these memory safety issues, but also compels us to explicitly address them.

This simple example shows that mutable iterators for recursively-typed structures like trees and graphs can’t be implemented in this way in Rust. We can’t solve the problem the same way that we did in a GC-ed language like Python.

Appeasing the Compiler

The key insight to solve this problem is that in our current setup, we have to acquire a number of borrows just to get a given node in the tree. For example, to access any given leaf, we have to first borrow all of its ancestor nodes.

If we can eliminate this property, and be able to randomly access each node, then we can make each reference to a node independent of another. This way, we won’t need multiple borrows to get one node, and we won’t need to keep multiple borrows in the iterator’s stack.

We need to add a level of indirection so that borrows are independent of each other, and each node can be accessed without having to use other node references.

Arena Allocators

Region-based memory management has existed long before Rust, but this was the first time I’ve ever encountered it. To put it simply, we’ll use a memory management tool called an arena allocator to introduce the indirection we require. The arena will be the owner of all of the tree nodes, and when it’s freed all the allocated nodes will be freed as well.

Every time we add a node to the tree, we’ll insert it into the arena, and get an index to the data back. To access a tree node, we just have to look it up in the arena using the index.

Our tree structure will then just be composed of an arena and the root index, with each node holding the indices to its children instead of references. In this way, we’ve made each node randomly accessible through the arena allocator, thus making each borrow of a node independent of another.

The simplest arena allocator is just a Vec.

Tree Node

We’ll alias the usize type as our TreeIndex, just to make usage of the index visually distinct from other types.

 1pub type TreeIndex = usize;
 2
 3pub struct TreeNode {
 4    pub value: usize,
 5    pub left: Option<TreeIndex>,
 6    pub right: Option<TreeIndex>
 7}
 8
 9impl TreeNode {
10    pub fn new(
11               value: usize,
12               left: Option<TreeIndex>,
13               right: Option<TreeIndex>
14              ) -> Self {
15        TreeNode {
16            value,
17            left,
18            right
19        }
20    }
21}

Tree with a stable arena allocator

Our tree implementation is based on a stable arena allocator, so node removals from the arena will not affect other nodes. Normally, if we remove an item from a Vec, then it will shift all following values down, thus also changing their indexes.

We don’t want to invalidate indexes if we remove a node! By making a removal the same as nullifying the value at an index, we can make the arena stable to removals, and other indices will be unaffected.

Unstable arenas are viable, but require more complex logic. While it may be more memory-efficient to remove unused nodes from an arena, a single removal could potentially invalidate all indexes and for our case, will require us to update the left and right fields in every single tree node.

It certainly depends on your use case, but for now we’ll use a stable arena allocator due its simplicity.

 1pub struct Tree {
 2    arena: Vec<Option<TreeNode>>,
 3    root: Option<TreeIndex>
 4}
 5
 6impl Tree {
 7    pub fn new() -> Self {
 8        Tree {
 9            arena: Vec::new(),
10            root: None
11        }
12    }
13
14    pub fn iter(&self) -> PreorderIter {
15        PreorderIter::new(self.root)
16    }
17
18    pub fn set_root(&mut self, root: Option<TreeIndex>) {
19        self.root = root;
20    }
21
22    pub fn add_node(&mut self, node: TreeNode) -> TreeIndex {
23        let index = self.arena.len();
24        self.arena.push(Some(node));
25        return index
26    }
27
28    pub fn remove_node_at(&mut self, index: TreeIndex) -> Option<TreeNode> {
29        if let Some(node) = self.arena.get_mut(index) {
30            node.take()
31        } else {
32            None
33        }
34    }
35
36    pub fn node_at(&self, index: TreeIndex) -> Option<&TreeNode> {
37        return if let Some(node) = self.arena.get(index) {
38            node.as_ref()
39        } else {
40            None
41        }
42    }
43
44    pub fn node_at_mut(&mut self, index: TreeIndex) -> Option<&mut TreeNode> {
45        return if let Some(node) = self.arena.get_mut(index) {
46            node.as_mut()
47        } else {
48            None
49        }
50    }
51}

The remove_node_at function at line 28 showcases how to perform a stable removal, such that the other indices are still valid (special thanks to ssokolow for catching my mistakes here). The functions node_at and node_at_mut on lines 38 and 46, respectfully, show how to retrieve an indexed tree node immutably and mutably.

This by itself is nothing special, which is good! We’re just using a Vec to store our TreeNodes and then tracking the indices.

The Visitor Pattern

The iterator will only track arena indexes instead of borrows, and at every call to next, it will return an index to a node in the arena. But there’s one last thing we need to address for this to work: the iterator can’t hold a borrow of the arena.

Recall why our mutable iterator didn’t compile: we can’t mutably borrow a parent node if we also mutably borrowed its children. Likewise, we can’t mutably borrow the tree nodes from the arena if the iterator is already borrowing the arena first.

It’s important to realize two things:

1. The iterator only requires an immutable borrow because it’s only accessing the node fields, and never modifying them.

2. The iterator only requires this borrow when we need the next node to be returned, so we should let it borrow the arena just for that operation, and release the borrow when it’s done.

In order to apply these changes, we can’t use the Iterator trait from our previous implementations. We need to write a custom one.

The new iterator will take an immutable borrow of the tree on every call to next. This means that between calls to next, we can mutate the tree (and the arena by extension) however much we want, because the iterator won’t be borrowing it. But when we’re done and want the next traversed node, we get a new immutable borrow of the arena and give it to the iterator.

In this way, the iterator now always has the most recent view of the arena when getting the next node, and also doesn’t need to borrow the arena persistently.

Take special note of the new tree: &Tree parameter of the next function implementation on line 18, which is the immutable borrow being passed to the iterator.

Mutation-Agnostic Pre-order Traversal

 1pub struct PreorderIter {
 2    stack: Vec<TreeIndex>
 3}
 4
 5impl PreorderIter {
 6    pub fn new(root: Option<TreeIndex>) -> Self {
 7        if let Some(index) = root {
 8            PreorderIter {
 9                stack: vec![index]
10            }
11        } else {
12            PreorderIter {
13                stack: vec![]
14            }
15        }
16    }
17
18    pub fn next(&mut self, tree: &Tree) -> Option<TreeIndex> {
19        while let Some(node_index) = self.stack.pop() {
20            if let Some(node) = tree.node_at(node_index) {
21                if let Some(right) = node.right {
22                    self.stack.push(right)
23                }
24
25                if let Some(left) = node.left {
26                    self.stack.push(left)
27                }
28
29                return Some(node_index)
30            }
31        }
32
33        return None
34    } // immutable borrow &Tree ends here
35}

The downside to this approach would be that if I were to remove an edge as I’m traversing through the tree, the iterator might still continue through the original tree based on the indices that are on its stack. The next function can be modified to address this case, but I’ve not done that here in order to retain parity with the Python implementation.

One Last Test

Recall the different loop constructions we used in our immutable iterator test. Because we’re not using the traditional Iterator trait in our implementation, we can’t use the for loop construction, so we need to update both loops to use the while loop construction. This time, we’ll also be passing an immutable borrow of the tree into our call to next!

 1fn main() {
 2    let mut tree = Tree::new();
 3
 4    let a = tree.add_node(TreeNode::new(4, None, None));
 5    let b = tree.add_node(TreeNode::new(5, None, None));
 6    let c = tree.add_node(TreeNode::new(2, Some(a), Some(b)));
 7
 8    let d = tree.add_node(TreeNode::new(3, None, None));
 9    let e = tree.add_node(TreeNode::new(1, Some(c), Some(d)));
10
11    tree.set_root(Some(e));
12
13    let mut preorder = tree.iter();
14    while let Some(i) = preorder.next(&tree) {
15        let node = tree.node_at_mut(i).expect("node to exist at given index"); // mutable borrow starts here
16        node.value *= 10;
17    } // mutable borrow ends here
18
19    let mut preorder = tree.iter();
20    while let Some(i) = preorder.next(&tree) {
21        let node = tree.node_at(i).expect("node to exist at given index");
22        println!("{}", node.value)
23    }
24}

Try it for yourself.

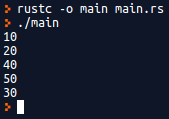
It works at last! 😄

Final Thoughts

We began with a trivial Python implementation of a pre-order traversal, and there were no frills or complexities. However, as soon as we started to port the same code over to Rust, we ran into issues starting with lifetimes, and then with mutable borrows.

These problems revealed memory-safety bugs in our ported Python code, which might have led to dangerous conditions somewhere down the line. Rust not only caught these mistakes, but forced us to address them.

In order to make the program memory-safe, we needed an entirely new approach using arena allocators and the visitor pattern. Even though it was different, the resulting code is just as readable and arguably just as simple as before. All we needed was a Vec and to tweak our iterator.

To be honest, when I first encountered these issues, it was incredibly frustrating. I started to really dislike the language. I couldn’t believe I was hitting roadblocks with such a seemingly trivial algorithm! And yet, implementing the solution in Rust has made the code more robust and safe. Now we could even go back and rewrite the Python code in the same memory-safe way that we’ve done here.

I think Rust could be the future of low-level programs that require execution speed and memory efficiency. It has its place alongside C++, but I think it’s much better positioned in the long run to entice young developers like myself. Just like Go, it’s a small language with a great foundation. But if I can’t afford a GC, I’m going with the language that guarantees my code is memory-safe!

Also, thank you to the Rust Discord members who patiently answered my questions and directed me to the visitor pattern.

Next Steps

There are still some exercises that I didn’t cover here that are left to the reader to explore on their own. The implementation I’ve shared above is mostly a toy one; a more serious program might use a library instead of writing everything from scratch. Also, there are better arena allocator implementations out there than just a Vec.

In the future, consider the following exercises:

1. Use a proper arena allocation library for more serious use cases like bumpalo, typed arena, or generational arenas
2. Port the Rust code back to Python
3. Try implementing graph traversal algorithms using arena allocators and the visitor pattern